Configuration interface.One thing I took along from last year’s ApacheCon was the idea to combine Apache Solr along with some mathematical search algorithms to figure out boost factor values. I did some work on that back then and on the way to this year’s BerlinBuzzwords. Now I finally have a proof-of-concept working which I’d like to share. If you want to have a look right away - the code can be found on Github.
The problem to solve:
When running search indexes with Solr, one thing you might stumble opon is that you’ve various fields in your documents and you’ve to adjust their weights to get reasonable results. Finding those “boosting” values can be quite complex when you have many fields and many scenarios. Usually getting the values right is a task for very experienced integrators.
/solr/select?defType=dismax&q=my+query
&qf=title^**42**+description^**23**+footnotes^**5**+dalmatiners^**101**+foo^**9001**+comments
Looking at it from a more technical perspective - when your Solr query looks like the one above, the question you’ve to answer is how the values for the highlighted numbers should look like to get reasonable results.
Measuring “reasonable”:
In order to solve the problem, the first thing we’ve to do, is to answer what we expect the outcome to look like. In other words, we’ve to measure how reasonable a specific solution is. For a search engine this can be done with some sample queries and some expectations along with that. The expectation could come in a form that we explicitly tell which documents we expect in the result lists of specific queries (and at predefined positions). Once we’ve these expectations, we can simple test agains the expectations and check whether or not specific boost factor values actually satisfy them.
A small example on that: In case we’ve a sample query with the expectation that document 123 appears in the first position and document 248 appears second. We could run this with two specific boost factor combinations (a) and (b). Along with (a) we might find that, document 123 actually ranks on position 8 and document 248 is found on position 4 and with (b) we’d find them on pos. 2 and pos. 14 - which one would we consider to be better?
Comparing the “error” and “squared error” produced by (a) and (b) gives us a possible hint:
- (a): 8-1 + 4-2 = 7+2 = 9
- (8-1)² + (4-2)² = 49+4 = 53
- (b): 2-1 + 14-2 = 1+12 = 13
- (2-1)² + (14-2)² = 1+144 = 145
While it’s not clear to compare both with just the normal error value comparision, the squared error shows clearly that (a) seems to outperform (b) in those cases and we should choose (a) for further considerations.
Being able to determine the “error” introduced by a specific solution then enables us to compare various solutions and helps us to play around with all sorts of optimizations.
The idea:
With a defined “cost function” like the one I introduced before, you’d be able to tackle the problem with some well known algorithmic solutions. Considering the boost factors to be represented as numerical vectors, we could use gradient methodologies to find good solutions. But having 20-40 fields per document would require to “search” a large numerical space and with gradient methods, this would result in a large amount of queries.
Another approach to run these optimizations, is to utilize genetic algorithms which kind of help to find good solutions within predictable amounts of time. You might know genetic algorithms for some lectures where people solved traveling salesman problems and actually the only change you’d have to make is to exchange the traveling salesman cost function with the cost function you saw before and you’d be close to a solution already.
With some more details: Genetic algorithms take an amount of randomly generated possible solutions (called the population) and try to find good solutions by applying the typical methods you know from your biology class (mutations, crossovers, natural selection). Natural selection is done in a way that from each generation only the top 50% “survive and the rest of the population is filled up with now solutions generated through mutations (random parameter changes of existing solutions) and crossovers (interchanging parts of two existing solutions to create a third one). All solutions are always measured and compared on their response to the defined cost function and this way we’re always able to determine the “best known solution” even after very short time.
If that sounds too high-level. For the shown query from above, the vector [42,23,5,101,9001,1] is the vector I used. In addition let’s considering we have another vector [1,1,1,1,1,1] with equal weights for all fields. Assuming those are our fittest vectors at a given time, we could derive new possible solutions by mutating them (e.g. [42,23,5,101,9001,1] ~> [42,23,5,101,505,1] ) or creating a cross-over between both ( [42,23,5,101,9001,1] & [1,1,1,1,1,1] ~> [42,23,5,1,1,1]). Even adding new random vectors to our population might add some value. Once we found enough new vectors to have a population of a decent size, we’d compare the fitness and keep only the top 50% and continue our process until we reach convergence or a fixed iteration limit.
A drawback of the genetic algorithm is that it might not deliver the optimal result, because it never found it. But that’s just how nature works too. So it’s more that you’ve to sacrifice “training runtime” over accuracy or vice versa.
Implementation:
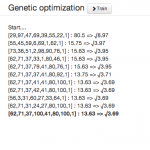10 generation optimizationThere’s really not too much to say other than that the code can be found in Github. I used NodeJS with ExpressJs, SocketIO and an Twitter Bootstrap interface to have a relatively good looking and somewhat performing proof-of-concept. I used that setup, because NodeJS seems to me as the most easiest way to talk to Solr and it “promises” to be performant even with larger examples. SocketIO helped a lot to ease the pain when it comes to Server <> Client communication. The only drawback of that setup is the that everything had to be turned into something which is able to deal with asynchronous processing. This makes the algorithmic parts look a bit odd and bloated - but for me the benefits outweigh the odds.
Final thoughts:
The proof-of-concept, which you’ll find on the Github repository, demonstrates that such type of optimization can work and that’s more or less all I wanted to do with it.
You can use the NodeJS tool with any of your Solr indexes and just go ahead and try it yourself. There are many parts which aren’t too accurate yet, especially the measuring could maybe done better with precision and recall measurements - but I assume that any type of cost function would work for now, that’s why P/R wasn’t implemented along with the tool. Also I’m not a NodeJS expert and the code might not follow best practice atm. - I’d be very happy to change that if anyone is interested to help?
When I did a small presentation during the Berlin Buzzwords bar camp I also got some other questions which don’t necessarily relate to just this implementation but to all sorts of automated optimizations.
The first question was, how to get the list of example queries and the “expected” documents for them. For now I assume that most applications at least know their top 50 or top 100 search and they should be able to predefine “relevant” documents for those searches. That’s at least what I assume everyone should have. Another way to generate the test data is to do some log file analyses and check the search and pick/weight the documents people clicked from within the results. This should also help to get some results.
Another questions related to that was wether long tail would fall behind with that approach. As this is only a proof-of-concept, I wasn’t really able to answer this. But I assume that long-tail searches would still benefit a lot more from the relevance certain documents gain due to high TF-IDF scores and those should then outweigh the “scoring bias” in a way. Another approach (known from machine learning) could be to leave out the top 1% of the documents (and searches) and just optimize for the rest of the top X% and afterwards check wether the top 1% still performs good - this way long tail could be “protected a bit more.
And the last question was whether I tested other (gradient based) algorithms already. The answer was and is, no. So far this only ran on my MacBook and I really didn’t want to benchmark my CPU. The code itself is somewhat prepared to take other optimization methods but I didn’t add in others. If you’re interested to do so - I’d be happy to accept your pull-requests.